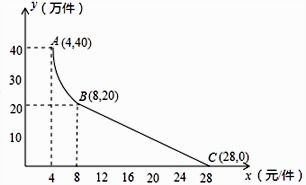
某公司銷售一種新型通訊產(chǎn)品，每件產(chǎn)品的進(jìn)價(jià)為4萬(wàn)元，每月銷售該產(chǎn)品的總開支（不含進(jìn)價(jià)）為11萬(wàn)元。在銷售過(guò)程中發(fā)現(xiàn)，月銷售量y（件）與銷售單價(jià)x（萬(wàn)元）之間存在如圖所示的一次函數(shù)關(guān)系。假設(shè)該一次函數(shù)關(guān)系為 y = kx + b，其中k和b為常數(shù)。通過(guò)分析，我們可以推導(dǎo)出月利潤(rùn)函數(shù)。

設(shè)月利潤(rùn)為P（萬(wàn)元），則P = (x - 4)y - 11。將y代入，得 P = (x - 4)(kx + b) - 11。為了最大化利潤(rùn)，需要根據(jù)實(shí)際數(shù)據(jù)確定k和b的值，并求解P的極值點(diǎn)。通常，在真實(shí)場(chǎng)景中，圖示的一次函數(shù)關(guān)系會(huì)顯示銷售量隨單價(jià)增加而減少（k < 0），這符合市場(chǎng)需求規(guī)律。通過(guò)優(yōu)化銷售單價(jià)，公司可以平衡銷量和單價(jià)，實(shí)現(xiàn)最大利潤(rùn)。